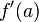 ou por
ou por  .*logx/x[n]*p * [lal]*para cada ponto temos uma forma geométrica.
.*logx/x[n]*p * [lal]*para cada ponto temos uma forma geométrica.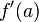 ou por
ou por  .*logx/x[n]*p * [lal]*R.
.*logx/x[n]*p * [lal]*R.p = progressões.
lal = latitude, longitude , altura.
 *logx/x[n]*p * [lal]*R
*logx/x[n]*p * [lal]*R *logx/x[n]*p * [lal]*R.
*logx/x[n]*p * [lal]*R. *logx/x[n]*p * [lal]*R.
*logx/x[n]*p * [lal]*R.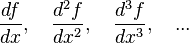 *logx/x[n]*p * [lal]*R.para cada ponto temos uma forma geométrica.
*logx/x[n]*p * [lal]*R.para cada ponto temos uma forma geométrica.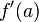 ou por
ou por  .*logx/x[n]*p * [lal]*R.
.*logx/x[n]*p * [lal]*R.p = progressões.
lal = latitude, longitude , altura.
 *logx/x[n]*p * [lal]*R
*logx/x[n]*p * [lal]*R *logx/x[n]*p * [lal]*R.
*logx/x[n]*p * [lal]*R. *logx/x[n]*p * [lal] *R.
*logx/x[n]*p * [lal] *R.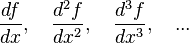 *logx/x[n]*p * [lal]*R.
*logx/x[n]*p * [lal]*R.p = progressões.
lal = latitude, longitude , altura.
 *logx/x[n]*p * [lal]*R
*logx/x[n]*p * [lal]*R *logx/x[n]*p * [lal]*R
*logx/x[n]*p * [lal]*R *logx/x[n]*p * [lal].*R
*logx/x[n]*p * [lal].*RR = ROTAÇÃO.
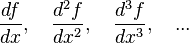 *logx/x[n]*p * [lal].
*logx/x[n]*p * [lal].
Nenhum comentário:
Postar um comentário